Stereoview of Mn2O6 )
Tl2Mn2O7 has the pyrochlore structure. This structure (Space Group Fd-3m, #227) contains
eight formula units per unit cell. As will be discussed below, Tl2Mn2O7 can be written as
(Mn2O6)(Tl2O') because its structure can be described in terms of two interpenetrating sublattices,
Mn2O6 and Tl2O'. The structure is significantly more complex than the three structures discussed so
far. It is convenient to decompose the structure of Tl2Mn2O7 into Mn2O6 and Tl2O' sublattices, load
sublattice data from files, analyze them separately, and finally examine the whole structure.
Understanding the Mn2O6 substructure
Load the Mn.CI file (in the CAESAR\Examples\Chapter3\Ti2Mn2O7 subdirectory) into Builder and display the crystal structure. In order to put the atoms inside the unit cell box, the user may employ the Into Unit Cell Box option of the Convert Unit Cell command. However, this operation will cut some Mn-O bonds lying outside the box and as a consequence generate unconnected O atoms inside the unit cell box. To avoid such a displeasing structural view, it might be better to employ the following procedure: (1) Select all atoms lying outside the box except for those making bonds with the Mn atoms lying on and inside the unit cell box. (2) Then use the Translate Atom Group... command to translate the selected inside the unit cell box. The translation vector can be readily found by rotating the structure and generating its view along the unit cell vector directions. The following figure presents a view of the structure thus obtained. The sublattice has eight Mn2O6 units per unit cell.
The user can eventually verify by extending the crystal structure that the Mn2O6 substructure is made up of corner-sharing MnO6 octahedra, that each MnO6 octahedron shares its corners with six other MnO6 octahedra, and that the MnO6 octahedra form a diamond network. Topologically, each MnO6 octahedron of the Mn2O6 sublattice corresponds to the midpoint of each C-C bond of the diamond lattice with a three-fold rotational axis of each MnO6 octahedron coinciding with the C-C bond axis. As an example of illustrating these points, one might extend the crystal structure and select all the atoms surrounding one Mn atom within a certain radius such that the selected atoms will consist of one MnO6 octahedron surrounded by its six nearest-neighbor MnO6 octahedra. For this purpose, first extend the structure in all three directions (e.g., -0.5 - 1.3 in fractional unit), then choose a central Mn atom, identify its atom attribute (e.g., Mn-1-1), and find the radius of the sphere (centered at that Mn) that will exclude all atoms but those belonging to the six nearest-neighbor MnO6 octahedra surrounding the central Mn atom. These steps are facilitated by zooming-in the central part of the extended structure. The proper radius can be determined in a trial-and-error manner by choosing a radius and looking at the selected atoms until the right value is found. Alternatively, it can be determined by first finding one of the outermost oxygen atoms from one of the six nearest-neighbor MnO6 octahedra of the central Mn atom and then calculating its distance to the central Mn atom using the command Atoms Environment. Either way the proper radius is found to be 5.4 Å.
Understanding the Mn2O6 substructure
Load the Mn.CI file (in the CAESAR\Examples\Chapter3\Ti2Mn2O7 subdirectory) into Builder and display the crystal structure. In order to put the atoms inside the unit cell box, the user may employ the Into Unit Cell Box option of the Convert Unit Cell command. However, this operation will cut some Mn-O bonds lying outside the box and as a consequence generate unconnected O atoms inside the unit cell box. To avoid such a displeasing structural view, it might be better to employ the following procedure: (1) Select all atoms lying outside the box except for those making bonds with the Mn atoms lying on and inside the unit cell box. (2) Then use the Translate Atom Group... command to translate the selected inside the unit cell box. The translation vector can be readily found by rotating the structure and generating its view along the unit cell vector directions. The following figure presents a view of the structure thus obtained. The sublattice has eight Mn2O6 units per unit cell.
The user can eventually verify by extending the crystal structure that the Mn2O6 substructure is made up of corner-sharing MnO6 octahedra, that each MnO6 octahedron shares its corners with six other MnO6 octahedra, and that the MnO6 octahedra form a diamond network. Topologically, each MnO6 octahedron of the Mn2O6 sublattice corresponds to the midpoint of each C-C bond of the diamond lattice with a three-fold rotational axis of each MnO6 octahedron coinciding with the C-C bond axis. As an example of illustrating these points, one might extend the crystal structure and select all the atoms surrounding one Mn atom within a certain radius such that the selected atoms will consist of one MnO6 octahedron surrounded by its six nearest-neighbor MnO6 octahedra. For this purpose, first extend the structure in all three directions (e.g., -0.5 - 1.3 in fractional unit), then choose a central Mn atom, identify its atom attribute (e.g., Mn-1-1), and find the radius of the sphere (centered at that Mn) that will exclude all atoms but those belonging to the six nearest-neighbor MnO6 octahedra surrounding the central Mn atom. These steps are facilitated by zooming-in the central part of the extended structure. The proper radius can be determined in a trial-and-error manner by choosing a radius and looking at the selected atoms until the right value is found. Alternatively, it can be determined by first finding one of the outermost oxygen atoms from one of the six nearest-neighbor MnO6 octahedra of the central Mn atom and then calculating its distance to the central Mn atom using the command Atoms Environment. Either way the proper radius is found to be 5.4 Å.
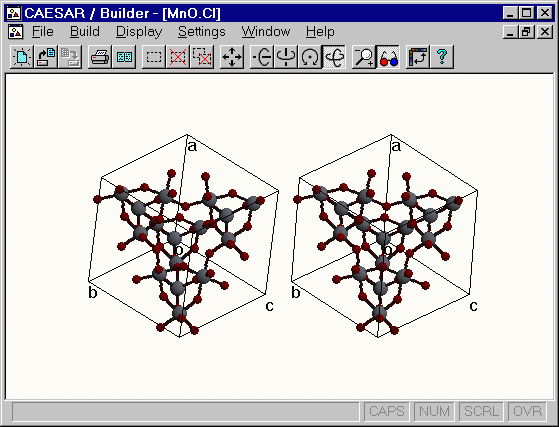
Figure. Stereoview of the unit cell of the Mn2O6 sublattice of Tl2Mn2O7.
Go back to The Gallery